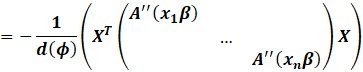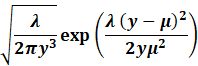Generalized Linear Models

Home

Generalized Linear Models extend the common Linear model to many other functions.

Logistic Regression models (0,1) binary responses, Poisson Regression models (Z+) count data,

Multinomial Logistic Regression models class binary responses and theres many more!

One issue of GLMs is that its pretty vague on how to estimate the parameters, other than just to use

pre-packaged solutions. I will aim to explain how to find the parameters clearly and succinctly.

https://en.wikipedia.org/wiki/Generalized_linear_model [Generalized Linear Model]

https://en.wikipedia.org/wiki/Natural_exponential_family [Natural Exponential Family]

https://www.sagepub.com/sites/default/files/upm-binaries/21121_Chapter_15.pdf [Textbook]

https://www.statsmodels.org/stable/glm.html [Statsmodels]

Canonical Form and Derivatives

GLMs are part of the exponential family.

This means all response variables can be written as:

Where we see that:

Then, we need to find the derivative. Firstly, note the identities:

So, we then find see that:

Now, if T(y) is the identity, ie T(y)=y, then we can simplify further:

Notice how it is always possible to express the natural parameter in terms of just theta.

Hence, if we show that:

Now, to find the variance of y, we use the second derivative property.

We use the chain rule ie df = uprime * v + u*vprime.

Notice once again the derivative of b is 1 since we can transform the function to be that way.

Likewise, T(y)=y.

But notice that A prime = E(y)!

Likewise, notice the definition of the variance!

Hence finally we have that given the canonical exponential family:

With that in mind, we have the log likelihood, and the canonical link:

Then, we use the Fisher Scoring / Newton Raphson algorithm:

However, in general, to account for the non canonical forms of the exponential family, we have that:

Link Functions

Here, we list a table of all popular link functions and their properties.

Reminder that

Name	Range, Usage
Logit
Inverse
Square Root
Inverse Squared
Identity
Log
Complementary Log Log
Negative Binomial
Relu
Softplus

Exponential Family Distributions

Here, we list a table of all popular exponential family distributions.

We also list the possible link function combinations.

Likewise, the color coded box indicates that the links are stable and give sensible results.

Reminder that

Name	Distribution	Range
Poisson
Gaussian
Gamma
Bernoulli
Inverse Gaussian
Negative Binomial

Name	Logit	Inv	Sqrt	InvSq	Id	Log	CLog	NBin	Relu	Soft
Poisson			X		X	X			X	X
Gaussian		X			X	X			X	X
Gamma		X			X	X			X	X
Bernoulli	X				X	X	X		X	X
Inverse Gaussian		X		X	X	X			X	X
Negative Binomial		X	X	X	X	X	X	X	X	X

Notice also that

Where the log gamma function is a common function in many programming languages.

Iteratively Reweighted Least Squares

The starting conditions for IRLS are set as:

Though for the binomial model, since the range is only from 0 to 1, then:

This means that NOTICE the negative sign

If IRLS is not feasible, as in if the time to solve a large p by p matrix is humungous:

One can also use general methods for optimization:

Likewise, one can use sketching to solve the system:

However, sketching can only be used if the weights are positive!!

Practical Models

There are some link function and family combinations that are just absurd.

So, we ignore these werido combinations.

Likewise, the power link functions are a bit redundant, since one can just use a power transform

to first transform the response variable.

Name	Range, Usage	Logit	Inv	Sqrt	InvSq	Id	Log	CLog	NBin	Relu	Soft
Poisson							X
Gaussian		X				X	X	X		X	X
Gamma
Bernoulli		X						X
Inverse Gaussian
Negative Binomial

Name	Range
Poisson
Linear
Log Linear
ReLU Linear
CLogLog Logistic
Logistic