Bag of Tricks

How do we train neural nets faster and correctly? Are there any heuristics we can use?

https://arxiv.org/abs/2004.01461 [Gradient Centralization: A New Optimization Technique for Deep Neural Networks (2020)]

https://karpathy.github.io/2019/04/25/recipe/ [A Recipe for Training Neural Networks (2019)]

https://www.tensorflow.org/tutorials/structured_data/imbalanced_data [Classification on imbalanced data]

Loss Accumulation

During training, its best one uses the batch loss and accumulate it so to save computation.

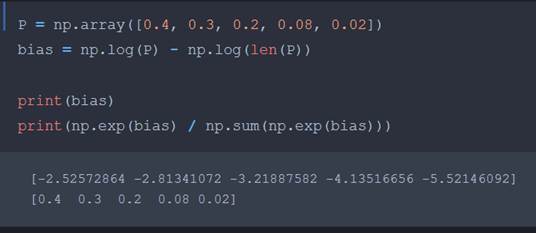
Bias Intialization

To attain superior accuracy / low loss, one must initialize the bias of the last layer appropriately!

Linear Last Layer

Sigmoid Last Layer

Softmax Last Layer

Notice epsilon since log(0)=inf.

K is number of classes

How did we derive the softmax bias initialization?

Iterate via coordinate descent, with b=0

We will find that after 1 iteration, convergence is seen. Then notice:

Where K is the # of classes.

Class Imbalance & Oversampling

A large problem in financial predictions (churn, fraud) is predicting imbalanced data.

This will be discussed more in the Generalized Linear Models chapter, but there are 2 methods to solve this problem:

Oversampling and Balanced Weighting.

In Balanced Weighting , one can use the weighting scheme from sklearn:

Then, to update the weights in gradient descent,

In fact, in linear models, this amounts to a weighted least squares regression:

Likewise, in GLMs using Newton s method:

However, it is well known that in minibatch gradient descent, its best one does Oversampling so to make learning easier.

To do this efficiently, we tack on the original indices the oversampled indices to balance the dataset.

So, we resample indices to match the maximum class frequency.

Learning Rate and Loss Plateaus

It is common that the loss will plateau. The issue is how does one detect when we can decrease the learning rate?

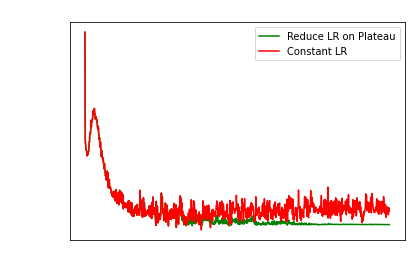
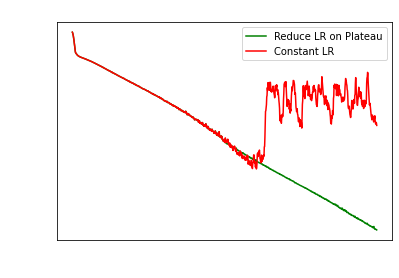
Blind-fully (like Keras and others) reducing the LR by 10 if the loss hasnt changed in 10 or 15 epochs is a bit silly.

Sometimes losses can fluctuate up and down, so we have to account for this.

Notice we find the difference between the EMA smoothed loss and the true batch loss.

This way, over 16 epochs, if the sum of the fluctuations of the loss is too small, (ie -100, 100, -100, 100) ,

then we decrease the learning rate by half. Notice 16 since even number.

Likewise, we increase the patience waiting time to not excessively reduce the LR.

Leslies Constant Relationship

Leslie Smith showcased that:

What this means if you increase the batch size by 2, you can increase the learning rate by 2!

Or increase weight decay by 2. Likewise, decreasing weight decay or the learning rate

has the same overall effect. Momentum is also an important factor, though not a lot, since its common beta1=0.9.

Standardization, Normalization

Pure momentum methods (like RAdam for the first N epochs) can struggle a lot when data is not standardized.

In fact, it is so bad, that RAdam can have exploding gradients!

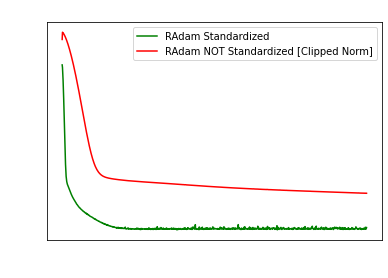
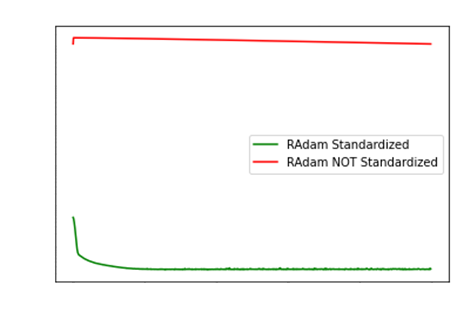
We already used gradient clipping (divide by norm) on the left. The right has NO gradient clipping, showcasing RAdam

failing dramatically… I have already contacted the original authors about this issue. https://github.com/LiyuanLucasLiu/RAdam/issues/54

More later in the RAdam chapter.

Also notice one doesnt have to directly store the standardized data, but rather, you only have to process a batch at a time.

Gradient Centralization

Finally, centralize gradients column-wise!!! We can do this on the fly.

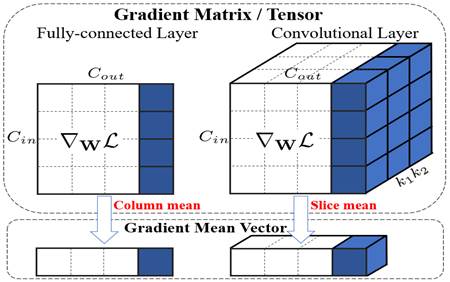
Illustration of the GC operation on gradient matrix/tensor of weights in the fully-connected layer (left) and convolutional layer (right).

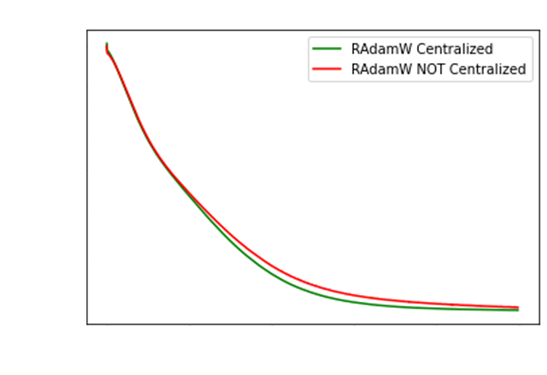
The RAdam paper also mentions gradient centralization as an important method to reduce variance at the start of training.

You can see the small improvement in loss when gradient centralization is used.