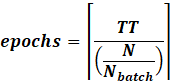Learning Rate Range Finder

How does one find the best learning rate? It is well known the learning rate is the single most important parameter

one must tune in order to get a good final result. Leslie Smith was the pioneer in the Learning Rate Range Finder,

and after FastAI edited it, it has become extremely useful!

https://arxiv.org/pdf/1506.01186.pdf [Cyclical Learning Rates for Training Neural Networks (2015)]

https://sgugger.github.io/how-do-you-find-a-good-learning-rate.html [Understanding the difficulty of training deep feedforward neural networks (2018)]

https://www.youtube.com/watch?v=bR7z2MA0p-o

Youtube video of Leslie Smith presenting his findings.

Essentially, start from a small learning rate (1e-7), then exponentially increase until a large one (10 or 100) for 200 iterations. Each time, you consume one mini-batch. Record the smoothed loss, and inspect the graph!

You can see the multiplication of the learning rate by the multiplier.

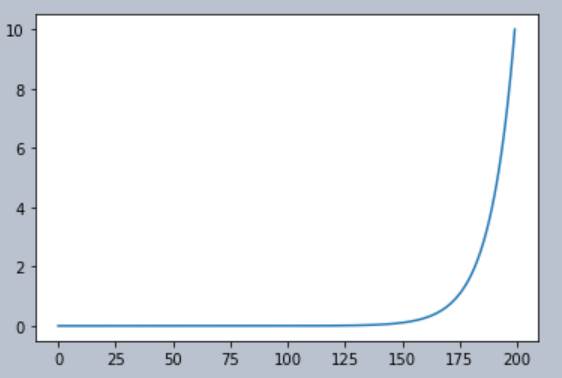
Essentially, Leslie Smith had linear steps. However, FastAI showcased that exponential steps is much better!

After plotting we get the plot below. You can see the typical horizonal S shape then a large

shot up of the loss. This is very typical.

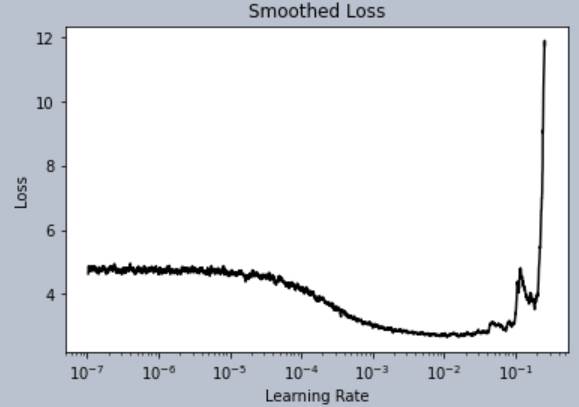
The next question becomes which is a good learning rate? One should select the rate halfway along the largest

downward slope. Ie, the steepest slope!

Strangely FastAI uses a gradient based approach to find the steepest slope. Sadly, I show that this is in fact

ineffective, at best only partially useful.

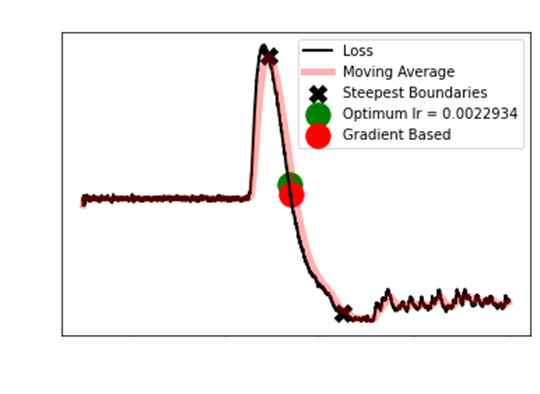
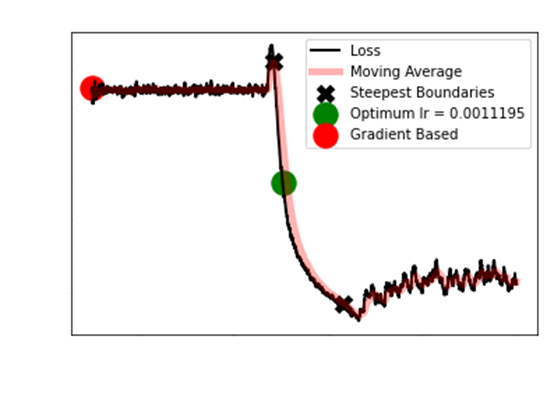
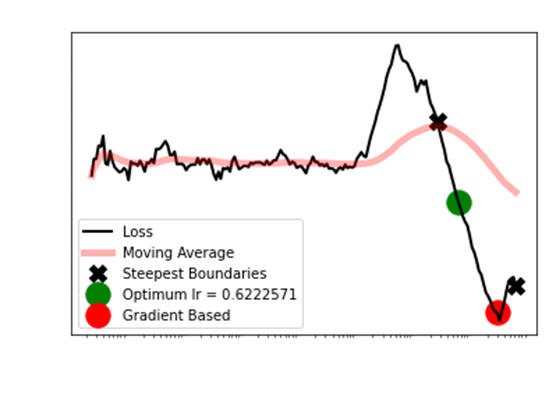
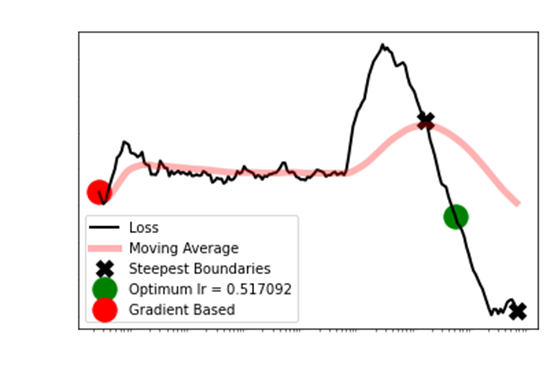
As you can see, the gradient based approach approach is atrocious. When the typical S then shoot up is not evident,

the FastAI approach actually recommends the worst learning rate. Even after removing the first 10 and last 5 observations,

it is clear the Longest Smoothed Chain method is optimum.

So what is the Longest Smoothed Chain method?

Smooth the loss with an exponentially moving average. Then, find the longest chain of the EMA that has negative gradient.

For in

So first, we have the exponentially moving average to remove random fluctuations.

Then, taking only O(N) time, we can find the longest chain of the moving average decreasing (ie the gradient based approach).

We do this by iterating from the left to right, with an inner loop to record the length of the chain.

Keep the chain with the largest negative gradient (L1 sum).

Notice 0.7 and 0.3. This is to shift the learning rate closer to the start of the steep slope.

For cyclical learning rates, the maximum and minimum learning rates are defined as:

We take the minimum of both quantities, since it might be that slope is so steep that one tenth of the

largest learning rate overshoots.

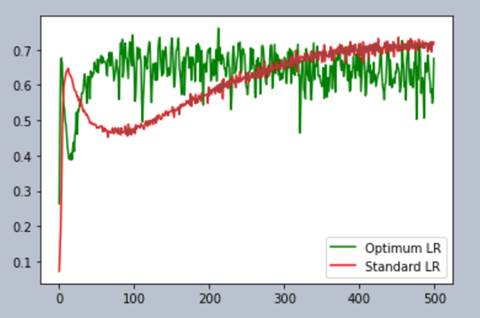
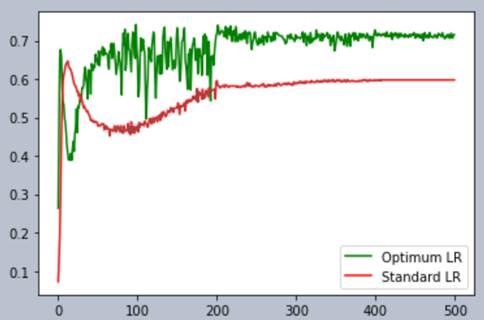
Its pretty clear choosing the correct learning rate speeds the convergence of training.

It takes over 350 to 400 epochs for the standard LR to reach the same accuracy as

100 or so epochs for the optimum LR!

You might have noticed the noisiness of the optimum LR. We can easily remove this

By decreasing the LR!